Grade (slope)
This article is for the grade of a topographic feature or constructed element, for other uses see: Slope (disambiguation)
The grade (also called slope, incline, gradient, pitch or rise) of a physical feature, topographic landform or constructed element, refers to the amount of inclination of that surface to the horizontal. It is a special case of the gradient in calculus where zero indicates gravitational level. A larger number indicates higher or steeper degree of "tilt". Often slope is calculated as a ratio of "rise" to "run", or as a fraction ("rise over run") in which run is the horizontal distance and rise is the vertical distance.
Grade or slope is applied to measuring existing physical features (such as canyon and hillsides, stream and river banks and beds), or in designing and engineering new elements for construction (such as roads, landscape and garden grading, roof pitches, railroads, aqueducts, and pedestrian-handicapped-bicycle circulation routes).
Contents |
Expression nomenclature
There are several systems for expressing slope:
- as an angle of inclination to the horizontal. (This is the angle α opposite the "rise" side of a triangle with a right angle between vertical rise and horizontal run.)
- as a percentage, the formula for which is
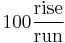 which could also be expressed as the tangent of the angle of inclination times 100. In the U.S., this percentage "grade" is the most commonly used unit for communicating slopes in transportation (streets, roads, highways and rail tracks), surveying, construction, and civil engineering.
which could also be expressed as the tangent of the angle of inclination times 100. In the U.S., this percentage "grade" is the most commonly used unit for communicating slopes in transportation (streets, roads, highways and rail tracks), surveying, construction, and civil engineering. - as a per mille figure, the formula for which is
 which could also be expressed as the tangent of the angle of inclination times 1000. This is commonly used in Europe to denote the incline of a railway.
which could also be expressed as the tangent of the angle of inclination times 1000. This is commonly used in Europe to denote the incline of a railway. - as a ratio of one part rise to so many parts run. For example, a slope that has a rise of 5 feet for every 100 feet of run would have a slope ratio of 1 in 20. (The word "in" is normally used rather than the mathematical ratio notation of "1:20"). This is generally the method used to describe railway grades in Australia and the UK.
Any one of these expressions may be used interchangeably to express the characteristics of a slope. Grade is usually expressed as a percentage, but this may easily be converted to the angle α from horizontal since that carries the same information.
There is a method in which slope may be expressed when the horizontal run is not known: rise divided by the hypotenuse (the slope length). This is not a usual way to measure slope. This follows the sine function rather than the tangent function and this method diverges from the "rise over run" method as angles start getting larger (see small-angle formula).
Many of the mathematical principles of slope that follow from the definition are applicable in topographic practice. In the UK, for road signs, maps and construction work, the gradient was traditionally expressed as a ratio such as 1 in 12, but signs showing gradient expressed as a percentage are becoming more common.[1]
In civil engineering applications and physical geography, the slope is calculated along a particular direction of interest which is normally the route of a highway or railway road bed.
Mathematical equations
Grades can be related using the following equations with symbols from the figure at top.
- Tangent as a ratio

This ratio can also be expressed as a percentage by multiplying by 100.
- Angle from a tangent gradient

If the tangent is expressed as a percentage, the angle can be determined as:

If the angle is expressed as a ratio (1 in n) then:
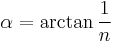
Roads
In vehicular engineering, various land-based designs (cars, SUVs, trucks, trains, etc.) are rated for their ability to ascend terrain. (Trains typically rate much lower than cars.) The highest grade a vehicle can ascend while maintaining a particular speed is sometimes termed that vehicle's "gradeability" (or, less often, "grade ability"). The lateral slopes of a highway geometry are sometimes called fills or cuts where these techniques have been used to create them.
Environmental design
Grade, pitch, and slope are important components in landscape design, garden design, landscape architecture, and architecture; for engineering and aesthetic design factors. Drainage, slope stability, circulation of people and vehicles, complying with building codes, and design integration are aspects of slope considerations in environmental design.
Railways
Gradients limit the load that a locomotive can haul, including the weight of the locomotive itself. On a 1% gradient (1 in 100) a locomotive can pull half (or less) of the load that it can pull on level track. (A heavily loaded train rolling at 20 km/hr on heavy rail may require ten times the pull on a 1% upgrade that it does on the level at that speed.) Early railways in the United Kingdom were laid out with very gentle gradients, such as 0.05% (1 in 2000), because the early locomotives (and their brakes) were so feeble. Steep gradients were concentrated in short sections of lines where it was convenient to employ assistant engines or cable haulage, such as from Euston to Camden Town, about 1.2 km. Extremely steep gradients need the help of cables, or some kind of rack railway.
Gradients can be expressed as W feet per mile, X feet per chain, 1 in Y, and Z%. Since surveyors like round figures, the method of express can affect the gradients selected.
The steepest railway lines that do not utilize a rack system include:
- 13.5 % - Lisbon tram, Portugal
- 11.6 % - Pöstlingbergbahn, Linz, Austria[2]
- 11 % Cass Scenic Railway USA (former logging line)
- 9.0 % - Ligne de Saint Gervais - Vallorcine, France
- 7.1 % - Erzberg Railway, Austria
- 7% - Bernina Railway, Switzerland
- 6.0% (1 in 16.6) - Docklands Light Railway, London, UK
- 5.6% (1 in 18) - Flåm, Norway
- 5.1% (1 in 19.6) - Saluda Grade, North Carolina, United States
- 5.0% (1 in 20) - Khyber Pass Railway, Pakistan
- 4.0% (1 in 25) - Cologne-Frankfurt high-speed rail line
- 4.0% (1 in 25) - Bolan Pass Railway, Pakistan
- 4.0% (1 in 25) (211.2 feet per mile) - Tarana - Oberon branch, New South Wales, Australia.
- 4.0% (1 in 25) - Matheran Light Railway, India [3]
- 3.7% (1 in 27) - Ecclesbourne Valley Railway, Heritage Line, Wirksworth, Derbyshire, UK
- 1.66% (1 in 60) Rudgwick platform with non-continuous brakes - too steep.
- 1.51% (1 in 66) ( foot per chain) New South Wales Railways, part of South line.
- 0.77% (1 in 130) Rudgwick platform with non-continuous brakes - not too steep.
It is customary for civil engineers to refer to the steepest grade on a section of rail line as the ruling grade for that section. Civil engineering works such as cuttings, embankments and tunnels are employed to reduce this maximum grade.
Compensation for curvature
Gradients on sharp curves are effectively a bit steeper than the same gradient on straight track, so to "compensate" for this and make the ruling grade uniform throughout, the gradient on those sharp curves should be reduced slightly.
Continuous brakes
In the era before continuous brakes, whether air brake or vacuum brakes steep gradients were a serious problem making it difficult to stop on the grade safely. In an extreme example, the Inspector insisted that a station be regraded before he would allow it to open. This required the gradient through the platform to be eased from 1 in 80 to 1 in 130.
See also
Effects of grade
The greater a grade, the more power an animal or a machine requires to climb it at a given speed; therefore routes with lower grades are preferred, so long as they do not have other disadvantages, such as causing the overall travel distance to increase significantly.
Vehicles proceeding up a steep grade demand more fuel consumption with typically increased air pollution generation. Sound level increases are also produced by motor vehicles travelling upgrade.[4]
See also
References
- ^ Highway code: Warning signs
- ^ "The New Pöstlingberg Railway" (PDF). Linz Linien GmbH. 2009. http://www.linzag.at/cms/media/en/linzagwebsite/dokumente/mobilittverkehr_1/pstlingbergbahn_1/folder_bergbahn.pdf. Retrieved 2011-01-06.
- ^ http://whc.unesco.org/en/tentativelists/2082/
- ^ C.Michael Hogan, Analysis of highway noise, Journal of Water, Air, & Soil Pollution, Volume 2, Number 3, Biomedical and Life Sciences and Earth and Environmental Science Issue, Pages 387-392, September, 1973, Springer Verlag, Netherlands ISSN 0049-6979
External links
- ^ Highway code: Warning signs
- ^ "The New Pöstlingberg Railway" (PDF). Linz Linien GmbH. 2009. http://www.linzag.at/cms/media/en/linzagwebsite/dokumente/mobilittverkehr_1/pstlingbergbahn_1/folder_bergbahn.pdf. Retrieved 2011-01-06.
- ^ http://whc.unesco.org/en/tentativelists/2082/
- ^ C.Michael Hogan, Analysis of highway noise, Journal of Water, Air, & Soil Pollution, Volume 2, Number 3, Biomedical and Life Sciences and Earth and Environmental Science Issue, Pages 387-392, September, 1973, Springer Verlag, Netherlands ISSN 0049-6979